Joseph Nicolas De Lisle

Route de la Comete observée à Paris en Aout, Septembre, Octobre et Novembre 1758. dans l'Observatoire de la Marine, à l'Hotel de Clugny Par M. Messier, Membre de la Société Royale de Londres, Presentée au ROY le 31 Octobre, et à l'Académie Royale des Sciences, dans son Assemblée Publique du 15 Novembre 1758. Par M. DE L'ISLE Astronome Géographe de la Marine et de l'Académie Royale des  Sciences et.

Tavola

La mappa illustra la "Memoire sur la cométe de 1758 par M. de l'Isle", memoria presentata da De Lisle il 15 Novembre 1758 e pubblicata nel 1765 in Mémoires, Académie Royale des Sciences, 1759.

Leggi l'intera Mémoire

L'autore effettivo delle osservazioni fu C. Messier che non era comunque titolato per presentare a suo nome le relazioni all'Accademia. Questa fu la prima di ventotto relazioni su comete che  Messier produsse tra il 1758 ed il 1788. Già da questa tavola appare evidente, nei titoli, anche il suo nome  quale autore delle osservazioni  e in qualche caso, per quelle successive,  si preoccupò di realizzare anche il disegno delle tavole annesse.

Nella tavola è trascritta l' orbita della cometa tra il 14 Agosto e il 2 Novembre 1758, la traiettoria del pianeta Venere dal primo Maggio al 7 Giugno dello stesso anno e la posizione e la data della prima osservazione che Messier fece della nebulosa posta subito a nord del corno meridionale del Toro. La nebulosa  porterà successivamente il numero uno (M1, la Nebulosa del Granchio, i resti ancora oggi visibili dell'esplosione della supernova del 1054) nel catalogo che l'astronomo parigino elencherà per distinguere quegli oggetti estesi e nebulosi che potevano essere in un primo momento confusi per delle comete.

La grande carta, 40,5x53cm, riporta inoltre in proiezione conica geocentrica la posizione di 131 stelle tratte dal catalogo di Flamsteed e ricalcolate da Messier per il 1758. Il reticolo evidenzia l'ascensione retta e la declinazione grado per grado ed è attraversato dalla linea dell'Eclittica che riporta la longitudine sempre alla scala di un grado. 

Titolo

Disegnatore ed incisore

Scala delle magnitudini stellari

La Nebulosa M1

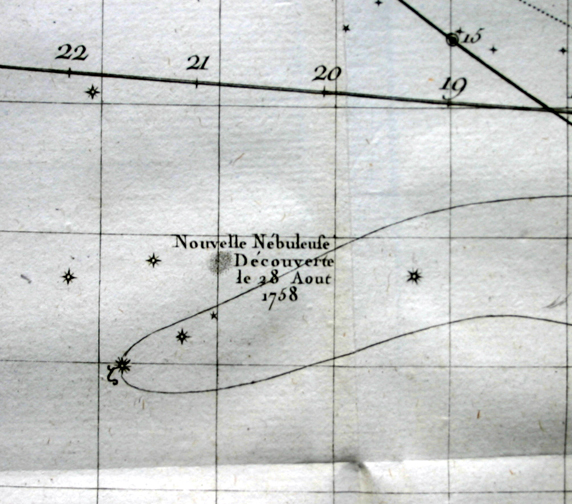
Messier osservò per la prima volta la nebulosa, poco prima dell'alba, la notte del 28 agosto del 1758, a pochi gradi dalla Luna calante. Ecco come De Lisle ricorda il fatto:"Ce qui l'eut de plus remarquable cette nuit, fut qu'en parcourant le ciel avec la lunette catadioptrique aux environs de la corne méridionale du Taureau, marquée x par Bayer, M. Messier y découvrit une lumière à peu près sembleable à celle de la Comète, mais qui était cependant plus vive, plus blanche & un peu plus élongée que la Comète qu'il oservait alors: cette Comète lui avoit paru toujours à peu près ronde   dans sa chevelure, sans apparence ni de queue ni de barbe. Comme la découverte de cette nouvelle lumière ou étoile nébuleuse ne se fit que vers la fin des observations de cette matinée...".

Si tratta però di una seconda scoperta indipendente in quanto l'astronomo inglese Bevis già l'aveva disegnata nel suo progettato e realizzato, ma mai pubblicato, atlante del 1750 ( Questo atlante è giunto a noi per l'esistenza fortunata di un numero limitatissimo di copie dell'intera tiratura che, per motivi del fallimento della tipografia che doveva stamparla, era stata requisita dalle autorità londinesi). 

Particolare della tavola del Toro dall'Atlante di Bevis dove è ben evidenziata la nebulosa

Orbita di Venere

Il pianeta Venere è descritto nella sua traiettoria mentre attraversa le stelle poste tra le corna del Toro tra il primo maggio ed il 7 giugno del 1758. E' curioso constatare che ricostruendo con un planetario moderno la zona del cielo interessata non si trova traccia del pianeta che invece si trovava nella costellazione dei Pesci. 

  Ecco la sua posizione per l'alba del 20 Maggio 1758 ricostruita con il Planetario Perseus

Da "Perseus", per cortesia Elitalia

Particolare delle Hyadi

La Mémoire fu pubblicata nel 1765 in

Consulta gli indici di tutti i volumi dell'

Histoire de l'Académie Royale des Sciences

 Mémoires de Mathématique et de Physique

Joseph Nicolas De Lisle

Per cortesia di 

Delisle ou De Lisle (Joseph Nicolas), astronome,  frère cadet de Guillaume, né à Paris le 4 avril 1688, mort à Paris le 11 septembre 1768. Il fit ses études au collège Mazarin, se passionna de bonne heure pour l'astronomie. Il semble, affirme Delambre, que c'est l'éclipse de Soleil de 1706 qui attira si fortement son attention, qu'elle lui inspira un désir extrême de pouvoir prédire ces phénomènes, et décida par là de ce  destin d'astronome! On nous dit dans son éloge qu'il inventa pour ainsi dire à cette époque l'astronomie sphérique et la gnomonique [1].

[1] Nous pouvons attester aussi, note encore Delambre, que nous avons trouvé à Dunkerque un tourier, nommé Garcia, qui avait fait à peu près de même. Pendant un assez long temps il avait marqué sur le périmètre de la tour les points où il voyait lever et coucher le Soleil; il suivait la marche des ombres, et sans avoir lu aucun livre, il était parvenu à construire sur l'un des murs de sa cabane, au haut de la tour, un cadran solaire vertical déclinant. II est vrai qu'il n'inventa pas la trigonométrie sphérique. Il nous demandait à être initié au calcul des éclipses. Nous avons vu depuis à Paris un meunier du Jura, qui toutes les nuits observait les levers et les couchers des étoiles; il en faisait de même le jour pour le Soleil, et de ses remarques il avait tiré une notion assez exacte de la situation de l'écliptique, qui tantôt fait avec l'horizon un angle très aigu, et tantôt un angle beaucoup plus considérable. Enfin d'après ses idées et quelques article d'almanach, il était arrivé à faire un Planétaire mu par un mécanisme imité de l'horloge de son village. Le ministre de l'intérieur l'avait fait venir à Paris avec sa machine; l'Académie nous chargea de l'examiner et d'en faire un rapport. Nos conclusions étaient que ce meunier était astronome à la manière des Chaldéens; qu'il méritait une gratification, mais que sa machine, comme son astronomie, arrivait 2000 ans trop tard et n'aurait mérité quelque attention qu'à Babylone, ou à Thèbes en Égypte. (Delambre).

On se doute bien qu'il en fut à peu près de même des premiers, essais de Delisle, et qu'il n'imprima aucun des ouvrages de sa jeunesse. Il s'adressa bientôt à Lieutaud, astronome de l'Académie, chargé alors de la Connaissance des Temps. Il fit, sous sa direction, des études plus régulières. Il obtint, en 1710, la permission d'habiter le dôme qui est au-dessus de la principale entrée du palais du Luxembourg. Deux ans après, il y plaça quelques instruments. En 1714, il entra à l'Académie des sciences, comme élève de Maraldi. En 1723, il était tombé de 20 pieds de haut en se préparant à une observation. L'énorme commotion qu'il reçut l'obligea pendant longtemps à garder la chambre. Deux ans après la tsarine  Catherine  de Russie l'attira à St Pétersbourg pour y fonder une école d'astronomie, et où il devint membre de l'Académie de cette ville (1727). On lui conserva d'abord sa place en France, et il ne perdit jamais sa charge de professeur royal au collège de France, qu'il céda longtemps après à Lalande. Cependant, tout occupé de ses devoirs de professeur, il fit en Russie bien peu de chose ou rien pour les progrès de la science ou pour sa réputation. Nous voyons seulement qu'en 1743, il envoyait à D. Cassini quelques idées sur une opération graphique propre à représenter les effets de la parallaxe dans un passage de Mercure. II donna par la suite plus de développements à ces premiers aperçus, et sa méthode, améliorée par Lalande, a été exposée par ce dernier fort clairement, au second volume de son Astronomie, et appliquée surtout aux passages de Vénus.

En 1741, l 'Académie, ennuyée d'une absence de seize ans, l'avait déclaré vétéran, et avait nommé à sa place, en ne lui conservant uniquement que le titre d'Académicien, c'est-à-dire le droit d'assister aux séances, quand il reviendrait, et celui de faire paraître ses mémoires parmi ceux des membres. II revint en effet le 15 septembre 1747. Nous verrons plus loin la conduite plus que singulière qu'il y tint à l'occasion de la comète  de 1759. Elle n'empêcha pas qu'en 1761 on ne lui rendit avec le titre de pensionnaire vétéran tous ses droits académiques, à la réserve de la pension effective. Il était revenu peu riche, et il avait employé ses épargnes à former, à l'hôtel de Cluny, un observatoire, qui devint célèbre par la suite, par les travaux de Messier. Il avait rapporté de ses voyages une ample collection de livres, de manuscrits, d'observations astronomiques et géographiques. Il céda le tout au dépôt général des cartes de la marine. La partie purement astronomique a été depuis transportée à l'Observatoire. Mais tentant d'amasser, on ne voit pas qu'il ait tiré grand parti de cette collection, qu'il pouvait consulter à chaque instant; et, d'après les témoignages de ceux qui l'ont vu, et quelques recherches faites par Delambre il a paru qu'après le peu qu'on en a tiré, le reste n'est guère qu'un objet de curiosité. Quoi qu'il en soit, il avait reçu en échange le titre d'astronome de la marine, avec un traitement de 3000 livres, 600 livres pour son secrétaire Libour, et 500 livres pour Messier, son élève. Peu de temps après, il céda à un élève plus ancien, le célèbre Lalande, sa place de professeur au collège de France; il se livra tout entier à des actes de dévotion et de charité; il mourut peu de temps après, entièrement oublié, et, sans deux de ses amis, Buache et Messier, qui se cotisèrent pour lui payer une fosse particulière, il eût été enterré comme un pauvre, dans la fosse commune; parce que des intrigants s'étaient emparés de ce qu'il pouvait avoir d'épargnes, au point qu'on ne trouva pas dans sa succession de quoi même payer l'enterrement le plus modeste. II eut pour élèves Godin, Grandjean de Fouchy, Lalande et Messier.

En 1715, quelques arrangements faits pour une princesse qui était venue loger au Luxembourg, forcèrent Delisle à porter ailleurs son observatoire; il se retira à l'hôtel Taranne, grande rue du même nom, dans l'appartement que Louville avait précédemment occupé. Il y fit quelques recherches sur, les bandes lumineuses qui bordent les ombres de tous les corps opaques. il donna à ce sujet un mémoire, où il rapporte dans le plus grand détail les mesures qu'il avait prises de ces ombres; il croit y voir des preuves de l'inflexion et pense qu'elles peuvent expliquer l'anneau lumineux qu'on a vu autour de la Lune, dans quelques éclipses totales de Soleil.

Étant encore en Russie, il avait lu à l'Académie de Saint-Pétersbourg, en 1733, un mémoire sur des thermomètres rendus universels, et qui marquaient en tout temps la quantité dont le mercure avait diminué, par la température de l'air, au-dessous de l'étendue qu'il a dans l'eau bouillante. Messier a eu longtemps un de ces thermomètres, tombés aujourd'hui en désuétude.

En 1714, il donna dans les Mémoires de l'Académie, sa méthode pour observer les solstices. Elle consiste à observer plusieurs déclinaisons, les unes avant, les autres après le solstice. Il y employait une grande lunette fixe, armée d'un micromètre. On n'a nul besoin des déclinaisons absolues, mais seulement de leurs différences, à l'aide desquelles on détermine l'instant du solstice, soit par interpolation, soit par la règle des carrés. Halley avait déjà proposé un moyen semblable et une construction géométrique de la solution. Nous avons déjà dit ce qu'on avait pensé de ce moyen, qui, quoique présenté deux fois, n'a jamais rien produit. Pour déterminer d'une manière fort incertaine l'instant du solstice, on négligeait l'obliquité de l'écliptique, à laquelle on s'attache aujourd'hui de préférence; quant à l'instant du solstice, dont on n'a aucun besoin, on le détermine bien plus sûrement par les longitudes calculées ou les ascensions droites observées.

En 1715; dans une occultation de Vénus, il aperçut distinctement une partie considérable du disque de la planète entrer sur celui de la Lune. Mais un mois après, dans une immersion de Jupiter au bord éclairé de la Lune , il n'aperçut nulle marque du disque de Jupiter sur celui de la Lune.

A propos de l'éclipse de Lune de 1717, il dit qu' il s'est servi d'un micromètre inventé par Lefèvre, où un cheveu sert d'index et se meut sur une ligne oblique divisée par des points, de sorte qu'en faisant varier cette obliquité, on change à volonté la valeur des parties du micromètre.. Cette idée pourrait avoir aidé J. Cassini pour la composition de son micromètre formé d'un losange dont on fait varier les angles. 

En 1718, il propose de changer la projection ordinaire pour le calcul des éclipses sujettes à la parallaxe. II rend son plan de projection parallèle à l'équateur, au lieu de le prendre perpendiculaire à la ligne qui va de la Terre au Soleil; par ce moyen, les différents parallèles de la Terre sont représentés par des cercles, sur lesquels les mouvements horaires sont uniformes. La ligne de latitude en conjonction et l'orbite seront des lignes droites qu'on pourra calculer et placer sur la figure. La Lune sera immobile au point de la conjonction. Les points de fin et de commencement, qui dans la projection ordinaire se trouvent sur la circonférence d'un cercle qui a pour rayon la somme des demi-diamètres, se trouveront à la périphérie d'une ellipse qui sera la projection à ce cercle; et pour déterminer les points d'intersection, on décrira une cycloïde allongée : idée bizarre à laquelle on n'a fait aucune attention, et qui n'en méritait véritablement aucune; elle ne faisait que déplacer la difficulté et multiplier les calculs. Le prétexte était que dans certains cas (toujours très rares) les variations des parallaxes de distances sont irrégulières, comme si l'on n'avait pas alors la faculté de réduire à rien les irrégularités, en prenant des intervalles plus rapprochés.

En 1719, fait la description d'une méridienne filaire. Nous en trouvons une de même genre à l'article Marinoni. Ces méridiennes sont passées de mode, et, l'instrument des passages le plus médiocre aurait un avantage marqué sur ce moyen si peu sûr. La même année, il répète des observations de réfractions : Il fait passer un rayon de lumière, dans un cylindre dans lequel il a opéré le vide. Il espérait obtenir une réfraction égale à la réfraction astronomique pour 45°; Mais jamais il ne put y parvenir.

Ici l'on trouve une longue lacune dans les Mémoires de l'Académie. Voyons ce que Delisle a fait imprimer en Russie :

Mémoires pour servir à l'histoire et au progrès de l'Astronomie, de la Géographie et de la Physique , par M. Delisle, professeur à Saint-Petersbourg, 1738, un vol. in-4°

Ce volume, qui devait être suivi de plusieurs autres, commence par une relation des aurores boréales, observées dans les parties septentrionales de la Russie , de 1727 à 1729, et d'autres observées à Pétersbourg depuis 1726 jusqu'en 1737. On y trouve ensuite des observations faites à l'observatoire du Luxembourg , dont il détermine la position. Il trouve la latitude 48° 51'0", et la différence des méridiens 0",2 occidentale. (Éphémérides de Lalande pour 1785, page lIX.)

Il donne les observations qu'il a faites de l'intervalle entre l'éclair et le bruit du tonnerre; puis sept observations d'une tache du Soleil. Pour en conclure les éléments, il trace un cercle dont il divise le diamètre en autant de secondes qu'il y en a dans le diamètre du Soleil en temps. Il place sur la figure les positions successives de la tache, d'après les différences observées d'ascension droite et de déclinaison. Après quelques opérations graphiques assez incommodes, il expose les règles de calcul, et commence par donner la règle véritable pour convertir en position héliocentrique la position géocentrique observée. Il est à remarquer que son élève Lalande a paru ignorer cette règle, ou du moins qu'il l'a négligée dans les deux premières éditions de son Astronomie. Delambre lui a fait corriger cette faute dans la troisième édition, en lui montrant qu'elle pouvait causer une erreur de 4 à 5° sur l'angle au centre du Soleil, entre la Terre et la tache.

Delisle détermine, comme on le fait encore aujourd'hui, trois, positions héliocentriques de la tache, et il est semble-t-il le premier auteur de cette méthode, inconnue dans l'école de Cassini.

Il joint les trois lieux de la tache par des arcs de grand cercle; il calcule le triangle formé par ces trois arcs. Sur le milieu. des côtés il imagine des arcs, perpendiculaires qui vont se couper au pôle de rotation. Il joint les pieds; des deux perpendiculaires par un arc de grand cercle. C'est la solution trigonométrique qui se présente le plus naturellement. Il ne fait que l'indiquer. Delambre l'a donnée avec tous ses détails. (Astron., tom. III, p. 19.).

Ensuite il calcule le problème par la projection orthographique, et trouve l'inclinaison 6°35', et le noeud en 1s 26°.

Par une autre tache qu'il a observée en 1714, Arago a trouvé : inclinaison = 5° 19'; nœud = 1s 25°35'5". Delisle ne les a pas calculées.

Après l'éclipse de Lune du 2 décembre 1713, il fait la remarque suivante : 

Depuis 4h 1/2 l'ombre a été très mal terminée, et toujours de plus en plus mal; ce qui vient sans doute de ce que la mer du nord était sur le bord de la Terre , dans ce temps-là, à l'endroit où la Lune était. En sorte que l'ombre de cette mer tombait sur la Lune. Ce qui confirme l'opinion de Clapiez, qui explique pourquoi le bord de, l'ombre qui paraît sur le bord de la Lune est, dans différents temps, plus ou moins confus, ou terminé, selon que ce sont des mers ou des continents qui jettent leur ombre sur la Lune. Si cette opinion était bien vérifiée, l'on en pourrait tirer deux avantages; car

1°) on pourrait reconnaître parmi les observations d'éclipses celles qui ont pu être observées exactement;

2°) on pourrait conjecturer l'existence des terres inconnues.

On trouve en différents endroits du volume des éclipses de tout genre, des mesures de diamètre, enfin des observations de plusieurs espèces; mais l'auteur n'y ayant joint aucune remarque, et n'en ayant déduit aucune conséquence, nous renverrons à son livre.

En 1748, dans une observation très incomplète de la grande éclipse de Soleil , il s'attache à noter les variations de température, et ce qu'on y voit de plus clair, c'est qu'il a senti l'effet du froid causé par l'éclipse, quoique le thermomètre n'ait éprouvé aucune variation. Il avait recommandé cette éclipse aux astronomes, par un avis imprimé, dans lequel il les exhortait à se procurer des éclipses artificielles, soit en couvrant d'un disque le disque du Soleil, soit en le couvrant d'un globe. Par ces moyens; ils verront une lumière très sensible qui colore le bord obscur du disque, dès que la lumière du Soleil s'en approche à la distance d'un douzième de son diamètre. La même apparence a lieu lorsque le Soleil est caché par des corps qui n'ont certainement aucune atmosphère, tels que les cheminées derrière lesquels le Soleil est caché momentanément. Il conseille aux astronomes de mesurer l'intensité de l'obscurité par les étoiles qu'ils pourront apercevoir; enfin il les exhorte à se tenir prêts à observer une comète, si par hasard elle se laissait voir pendant la plus grande obscurité.

Il parle, en 1749, d'un froid de -27° du thermomètre de Réaumur, à Pétersbourg le 27 janvier 1733. Celui de 1709 en France, n'avait été que de -15°,5. Depuis, à Pétersbourg, on a vu le thermomètre descendre à -30°. Au cercle polaire, les académiciens l'avaient vu à -37°. Enfin, le 16 janvier 1735, il descendit à -70° à Yeniseisk en Sibérie.

Dans l'éclipse de Lune de 1750, il observait au fil équatorial et horaire de sa lunette les passages du bord de la Lune et de celui de l'ombre.

Année 1755, il rapporte les observations qu'il a faites en 1718 des diamètres du Soleil avec une lunette de 20 pieds garnie de deux oculaires placés à côté l'un de l'autre. Ils lui paraissent plus petits de 10" qu'ils n'ont paru à Picard et à Cassini. Il dit qu'il a toujours trouvé les diamètres du Soleil de plus en plus grands à mesure qu'il employait de plus courtes lunettes.

Dans le passage de Mercure de 1756, il emploie la durée du passage, à la détermination du diamètre du Soleil, et trouve qu'il faut diminuer de 20" le diamètre des Tables de Halley. Cette durée est de 5h 30' dans le noeud ascendant et de près de 8 h dans le noeud descendant. Il calcule ces passages par les lieux héliocentriques, méthode adoptée depuis par Lalande, et dont on voit que Delisle est le premier auteur. Il suit d'ailleurs les règles de la projection orthographique. Il trouve ainsi que le diamètre du Soleil est de 31' 59" 84, par les observations d'Amiot, et de 7 à 8" plus grand par celle de Gaubil. Il paraîtrait résulter de cette différence que sa méthode n'est pas aussi sûre qu'il a l'air de le croire.

Ce mémoire paraît fait avec beaucoup de soin. L'auteur avait senti la nécessité de faire le calcul en entier avec la précision des centièmes de seconde. Il avait, en conséquence, mis cette précision dans la partie des tables de  Mercure qui lui était utile en cette circonstance. Il avait donc calculé l'équation du centre par les méthodes rigoureuses, mais 10 en 10' seulement. On a aujourd'hui des formules de mouvement horaire encore plus précises et qui exigent beaucoup moins de temps, on pourrait même calculer les effets d'une petite erreur dans l'excentricité et dans le lieu de l'aphélie.

Dans un long mémoire sur la comète de 1758, on ne voit que des positions d'étoiles; une carte du cours de la comète, et ses éléments calculés par Pingré.

Dans les mémoires de 1760, on en trouve un dans lequel Delisle, parlant au nom de Messier, raconte les préparatifs qu'il a faits pour apercevoir la comète de 1759 avant tous les autres astronomes. Il se vante beaucoup de ses succès. II est bien. vrai qu'il a vu la comète le premier, du moins en France ; mais c'est probablement que les autres astronomes s'étaient reposés sur lui. du soin de la chercher. Ils savaient que lui-même avait chargé de ce soin Messier, qui n'avait, rien autre chose à faire et qui réellement y perdit toutes ses nuits pendant plus d'un an. On était bien sûr que La Caille ne voudrait pas acheter à ce prix le plaisir d'annoncer la comète à ses confrères. Ce rôle convenait parfaitement à Messier, qui n'avait encore que ce moyen d'acquérir la bienveillance des académiciens. Les moyens de Delisle n'eurent d'autre effet que de retarder la découverte de plus d'un mois et d'empêcher tous les astronomes de Paris de s'occuper de cette recherche. En 1531, la comète n'avait été vue que 18 jours avant son périhélie; en 1607 elle se montra 33 jours avant le passage; en 1682, 24 jours seulement; mais dans ces diverses apparitions personne ne la cherchait, on l'avait vue quand elle était assez belle pour frapper des regards même inattentifs. Delisle conjecture qu'avec des lunettes on aurait pu la voir un mois avant le périhélie. Pour faciliter la recherche de la comète, il calcule son cours en supposant qu'elle pourra se voir 25 jours ou bien 35 jours avant le passage au périhélie. Ceci paraît supposer que l'on connaît l'instant du périhélie, et cet instant doit être changé par les perturbations. Si le dérangement était d'un mois, par exemple, on sent que la commutation de la comète étant augmentée ou diminuée de 30°, le lieu géocentrique pourrait être très différent.

Messier avait tracé sur une carte déleste ce double cours, formant deux courbes divisées en jours. Il joignait par des droites les lieux correspondants et parcourait avec sa lunette la ligne de chaque jour; et comme la comète était ailleurs, il était tout naturel qu'il ne l'aperçût pas.

Après bien de la peine et des recherches, continue Messier, j'en fus bien récompensé, ayant eu l'avantage de découvrir cette comète le 21 janvier 1759, cinquante jours avant le périhélie. Il ne dit pas que sans peine et sans recherche un paysan l'avait aperçue un mois plus tôt à la vue simple. il convient cependant que Delisle eût encore mieux réussi en se renferment dans des limites moins étroites. Messier donne ensuite les détails les plus circonstanciés de ses observations jusqu'au 4 février, ensuite il trace sur une carte la route sur laquelle on la reverra lorsqu'elle sera sortie des rayons du Soleil. il la retrouva le premier avril avec une queue de 25°, qui probablement lui fut plus utile que la route tracée d'avance dans des suppositions inexactes. A cette époque; Mayer écrivait à La Caille et à Delisle que la comète avait été vue et calculée en Allemagne. Delisle voyant qu' il n'était plus maître de son secret, permit à Messier de parler de ses observations à Le Monnier, Lalande et Pingré, qui procurèrent à d'autres la satisfaction de trouver cette comète le 2 avril. Il ne dit rien de la lettre qui avait procuré cette satisfaction à La Caille et ne songe pas que le besoin de s'assurer le secours des autres astronomes subsistait dès le mois de janvier, avec d'autant plus de force que l'observatoire de l'hôtel de Cluny n'était pas très avantageusement situé pour ces observations, et que Messier fut obligé d'abord de se transporter dans le jardin du Palais des Thermes, qui joint cet hôtel, et puis d'aller s'établir au collège de Louis-Le-Grand. Le reste du mémoire donne les observations que Messier continua jusqu'au 2 juin, 134 jours après sa découverte.

Delisle avoue en finissant que la comète a été vue les 25 et 26 décembre 1758 par un certain Palitzsch. Il a pourtant bien de la peine à concevoir comment cet observateur, qu'il décrit  donc (à tort) comme un simple paysan aura pu la découvrir à la vue simple, sans la chercher ni la soupçonner (ce qui était également faux), un mois plus tôt que Messier ne l'a vue à Paris, puisque le 21 janvier sa lumière était si faible qu'il n'était pas possible de l'apercevoir à la vue simple. Le mémoire est terminé par les observations étrangères, par des tables et des cartes.

Delisle, véritable auteur de ce mémoire, qu'il donne en partie pour l'ouvrage de Messier, n'y met d'ailleurs rien d'intéressant sur la comète; il ne fait aucun usage de ces observations dont il s'est réservé le secret. On n'a de lui aucune orbite de comète. Il paraît avoir eu par-dessus tout le goût des collections et des manuscrits, qu'il prisait plus à raison de leur rareté que de leur mérite réel. Au reste il n'était plus jeune, et jamais il ne paraît avoir été un calculateur bien courageux. Tout ce qui est resté de lui, c'est sa manière de calculer le lieu héliocentrique des taches, sa manière de calculer les passages de Mercure et de Vénus et de déterminer par la projection stéréographique les courbes d'entrée et de sortie pour tous les lieux de la Terre , méthode que Lagrange a depuis soumise au calcul, quoiqu'elle ne soit qu'approximative et qu'elle ne soit même bonne que pour faire des cartes; car pour choisir les stations les plus convenables, on le peut avec moins de peine au moyen d'un globe terrestre. (Delambre, 1827).

Delisle a publié de nombreux mémoires et notes dans les journaux et recueils scientifiques de son temps et a édité à part : Abrégé des mathématiques (Saint-Pétersbourg, 1728, 3 vol. in-8); Éclipses circumjovialium, etc. (Berlin, 1734, in-4); Mémoires pour servir à l'histoire et aux progrès de l'astronomie, de la géographie et de la physique (Saint-Pétersbourg, 1738, in-4); Mémoire sur les nouvelles découvertes au nord de la mer du Sud (Paris, 1752-53, in-4).

Leggi la voce Comet come appare nel

A New Royal and Universal Dictionary of Arts and Sciences, London 1770-1771, Printed of J. Cooke 

di

M. Hinde, W. Squire, J. Marshall, Thomas Cooke

www.atlascoelestis.com

di   FELICE STOPPA