Christiaan Huygens

Systema Saturnium, Sive De causis mirandorum Saturni Phaenomenon, Et Comite ejus Planeta Novo, Hagae MDCLIX

Phaenomenon in Orione novum

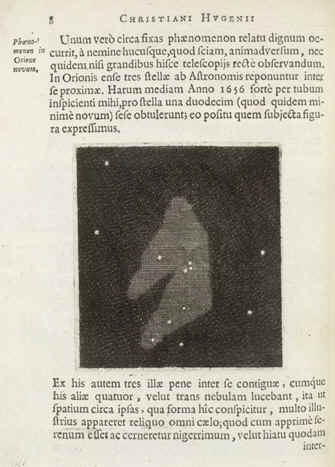
La carta che presento è inserita alla pagina otto del libro con il quale l’astronomo olandese tratta delle tre più importanti scoperte astronomiche della sua carriera di osservatore: La scoperta di Titano, il satellite maggiore di Saturno. Il riconoscimento che ciò che giace intorno al pianeta è un anello sottile e piatto, non collegato a Saturno, e inclinato rispetto all’Eclittica ed infine la Nebulosa, l’attuale M42, nella cintura di Orione, all’interno della quale riconosce, con l’ausilio del telescopio, sette distinte stelle, altre cinque, come risulta dall’esame della carta, sono poste all’esterno della massa gassosa. La carta, un quadrato di 10’ di arco di lato, è disegnata in proiezione concava.

Titolo

Tavola della Nebulosa di Orione

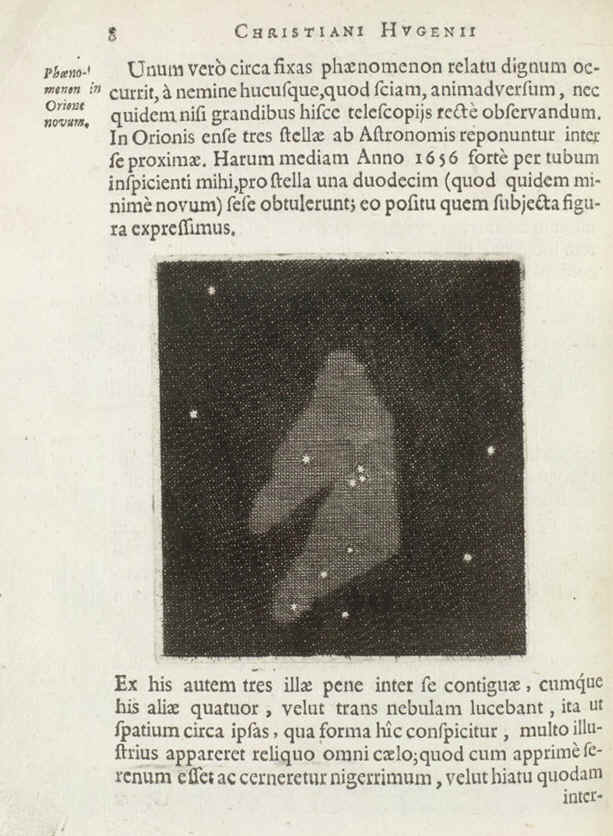
Tavole relative all'Anello di Saturno

Foto di Mauro Zorzenon

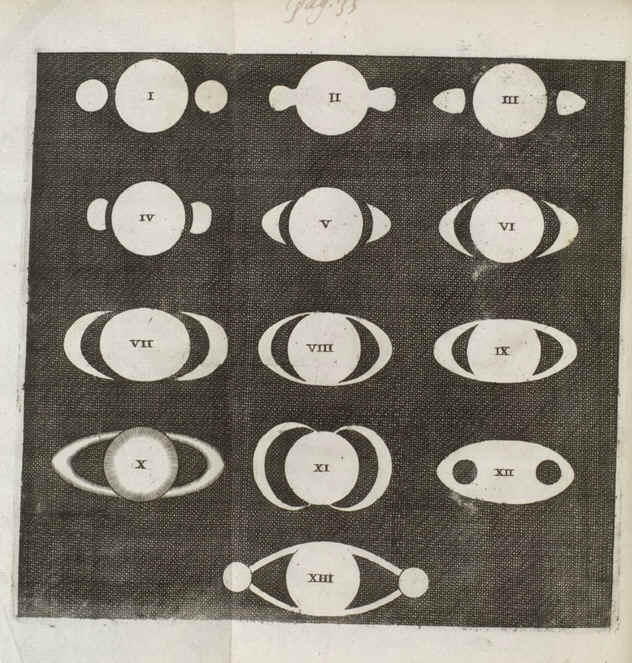
Tavola con le osservazioni storiche di Saturno prima della scoperta dell'anello

Alcune osservazioni di Titano

Le bande in Giove

La Grande Nebulosa di Orione

di

Mauro Zorzenon

La voce Huygens dall’ Enciclopedia Treccani

Huygens 〈hö´igℎens〉 (o Huyghens; orig. Hugens; latinizz. Hugenius), Christiaan. - Fisico, astronomo e matematico olandese (L'Aia 1629 - ivi 1695). Membro della Royal Society di Londra (1663) e dell'Académie des sciences di Parigi (1666), è tra i fondatori della meccanica e dell'ottica fisica. Suo padre Constantijn, diplomatico e segretario del principe d'Orange, era interessato alle scienze e alle arti, conosceva Descartes ed era in corrispondenza con Mersenne. Christiaan impressionò presto per i suoi progressi negli studî; a nove anni, già introdotto alla musica e alla matematica, parlava il latino e apprendeva altre lingue. Dal 1645 al 1647 studiò all'università di Leida dove ebbe come maestro Frans van Schooten, il primo commentatore della Géométrie di Descartes. Dal 1647 al 1649 passò a studiare retorica e diritto a Breda, al Collegio d'Orange. Rifiutandosi di seguire il padre nella carriera di funzionario, si applicò allo studio delle matematiche. I suoi primi interessi furono rivolti ai problemi sulla quadratura delle sezioni coniche a cui dedicò i Theoremata de quadratura hiperboles, ellipsis et circuli (1651) che contengono una confutazione della quadratura del cerchio di Grégoire de Saint-Vincent. Nel 1654 elaborò la teoria delle evolute ed evolventi delle curve, pubblicando il trattato De circuli magnitudine inventa. Nello stesso tempo attendeva alle osservazioni astronomiche con strumenti che egli stesso costruiva. Scoprì un satellite di Saturno (Titano, 1655-56) e ne individuò l'anello (1659). Riconobbe inoltre che la Luna è priva di atmosfera e che i suoi "mari" devono essere privi d'acqua. Intanto nel 1657, in appendice alle Exercitationum mathematicarum libri quinque di Schooten, H. pubblicava il suo Tractatus de ratiociniis in ludo aleae, opera di fondamentale importanza per il calcolo delle probabilità. L'anno successivo descrisse la sua invenzione dell'orologio a pendolo. Questo periodo fecondo di risultati comprende anche la scoperta del tautocronismo della cicloide (1659) e le ricerche sulla forza centrifuga. L'invenzione dell'orologio a pendolo e la scoperta dell'anello di Saturno gli assicurarono una celebrità europea. Nel 1660-61 e nel 1663-64 compì due viaggi a Parigi dove poi, su invito di J.-B. Colbert, si stabilì dal 1665 fino al 1681, a parte due soggiorni in Olanda per motivi di salute. Il suo soggiorno parigino non si interruppe nemmeno quando nel 1672 Luigi XIV dichiarò guerra all'Olanda nonostante i legami degli H. con il governo olandese. Nel 1673 H. dedicò a Luigi XIV la sua grande opera sull'orologio a pendolo, Horologium oscillatorium, sive de motu pendolorum ad horologia aptato demonstrationes geometricae, dove stabilisce la nozione di momento d'inerzia, i primi teoremi sulla meccanica dei sistemi rigidi e la teoria del pendolo composto. Attraverso queste ricerche e altre precedenti sull'urto fu condotto a enunciare, se pure per un caso particolare, il teorema delle forze vive, ad approfondire lo studio del moto circolare, a dare i teoremi fondamentali sulla forza centrifuga, infine a verificare le variazioni di gravità con la latitudine, proseguendo così le ricerche di G. Borelli e preparando la via a quelle di I. Newton. H. lasciò Parigi per L'Aia nel 1681 per motivi di salute senza farvi più ritorno. La morte di Colbert, protettore dell'Académie des sciences, e la revoca dell'editto di Nantes che assicurava ai protestanti francesi alcune libertà, non consentirono il suo ritorno a Parigi. Nel 1689 H. visitò Londra dove incontrò Newton. I Principia mathematica suscitarono in lui ammirazione, ma anche molte riserve che lo portarono a pubblicare, come supplemento al suo Traité de la lumière (1691), un Discours de la cause de la pesanteur. La preoccupazione teorica di H. nei riguardi dei Principia (condivisa allora da Leibniz e dai cartesiani) era che le ipotesi della gravità e dell'azione a distanza reintroducessero nella fisica le qualità latenti degli scolastici che il meccanicismo cartesiano sembrava aver espulso vittoriosamente dallo studio della natura. Gli ultimi anni della vita di H., tormentati da cattive condizioni di salute, furono caratterizzati dal suo interesse per i risultati del calcolo differenziale, le cui regole erano state pubblicate da Leibniz nel 1684 (buona parte dell'epistolario H.- Leibniz è successiva al gennaio 1688). H. fu stimatissimo dai suoi contemporanei e dagli scienziati della generazione successiva. Newton lo chiamava "Summus Hugenius", Leibniz lo metteva a fianco di Archimede, Keplero e Galileo, Descartes e Newton tra i massimi scienziati di tutti i tempi. Jacob Bernoulli dedicò la prima parte della sua Ars conjectandi (1713) alla trascrizione e al commento del De ratiocinis di Huygens. Anche in Italia la sua fama nello scorcio del Seicento fu superiore a quella di Newton e di Leibniz. H. fu anche un grande inventore che contribuiva personalmente a progettare e a perfezionare i suoi strumenti. Il suo metodo della scoperta si ispirava ai metodi archimedei e della Géométrie di Descartes. Una delle sue scoperte più famose, la determinazione dell'anello di Saturno, fu innanzitutto guidata dal suo tentativo di applicare la teoria cartesiana dei vortici al moto del satellite di Saturno, Titano. Proprio in confronto con Galileo e Descartes e Newton, tuttavia, l'opera scientifica di H. risultò sottovalutata non avendo dei primi il carattere innovativo, dell'altro la mirabile sistematicità. La sola nuova teoria generale che H. formulò fu la teoria ondulatoria della luce, che fu però messa in ombra per tutto il Settecento dall'ottica corpuscolare di Newton. Solo agli inizî del sec. 19º fu universalmente accettata perché consentì la spiegazione della diffrazione della luce e A.-J. Fresnel, nella sua Note sur la théorie de la diffraction (1818), poneva il principio di Huygens alla base della spiegazione dei fenomeni ottici. H. morì all'Aia l'8 luglio 1695. Postumi apparvero il trattato di cosmogonia Cosmotheoros, in cui H. si riallaccia alla teoria cartesiana dei vortici cosmici, e un trattato di ottica, Diottrica, in cui sono stabiliti, sulla base della teoria ondulatoria della luce, i principî della propagazione, riflessione e rifrazione di essa. Le opere di H. furono raccolte in una magistrale edizione critica, le Oeuvres complètes de Christiaan Huygens, publiées par la Société hollandaise des sciences (22 voll., 1888-1950).

Luigi Pepe

www.atlascoelestis.com

di  FELICE STOPPA

OTTOBRE 2013